31.
Solución
31. Cien Prisioneros
Un verdugo alinea a 100 prisioneros en fila india y les pone un sombrero rojo o azul en la cabeza. Cada prisionero puede ver los sombreros de las personas que están delante de él en la fila, pero no su propio sombrero ni el de los que están detrás de él. El verdugo comienza por el final (atrás) y pregunta al último prisionero el color de su sombrero. Debe responder “rojo” o “azul”. Si responde correctamente, se le permitirá vivir. Si da una respuesta incorrecta, lo matan instantáneamente y en silencio. (Aunque todos escuchan la respuesta, nadie sabe si la respuesta fue correcta). La noche anterior los prisioneros discuten sobre la estrategia para salvarse los máximos posibles. ¿Que deberían hacer?
Solución
La persona de atrás, llamémosle persona número 1, estará de acuerdo en que si ve un número impar de sombreros rojos, dirá rojo, si ve un número par de sombreros rojos, dirá azul. (Obviamente, cualquier esquema similar funcionaría, pero usaremos este). Desafortunadamente, esto significa que tiene un 50% de posibilidades de supervivencia, pero garantiza la de todos los demás.
Entonces todos, excepto la primera persona, sobreviven. Y habría sobrevivido si hubiera llevado un sombrero azul. Esto nos da una tasa de supervivencia esperada del 99,5% para 100 personas; o (n – ½)/n en el caso general
30. Reparto de panes
Había dos hombres comiendo. El primer hombre trajo cinco hogazas de pan y el segundo trajo tres. Un tercer hombre se unió a ellos y juntos se comieron los 8 panes enteros. Cuando se fue, el último les dio a los dos primeros hombres 8 monedas como agradecimiento.
¿Cuál debe ser el reparto justo de esas monedas entre estos dos hombres?
Solución
7 y 1
29. Avión con viento
Si un avión hace un viaje de ida y vuelta y sopla viento, ¿el tiempo del viaje es más corto, más largo o igual?
Solución
Entonces el tiempo total ha aumentado. Y esa es la respuesta a la pregunta. ¿Pero qué ha pasado? ¿Por qué no se cancelan? Pues simplemente porque el viaje contra el viento es más lento y dura más el avión va contra el viento durante más tiempo
28. Tres hombres en un hotel
3 hombres entran en un hotel. El hombre detrás del escritorio dice que una habitación cuesta 30 €, por lo que cada hombre paga 10 € y va a la habitación. Un rato después, el hombre detrás del escritorio se dio cuenta de que la habitación costaba solo 25 €, así que envió al botones a la habitación de los 3 chicos con 5 monedas de 1 €. En el camino, el botones no sabía cómo dividir las 5 monedas en partes iguales entre los 3 hombres, así que le dio a cada hombre 1 € y se quedó con los otros 2 €. Esto significa que los 3 hombres pagaron 9 € cada uno por la habitación, lo que es un total de 27 €, sumando los 2 € que se quedó el botones = 29 €. ¿Dónde está el otro euro?
Solución
No es sumando los 2 € del botones, sino restando los 2 €.
27 € (total) – 2 € (botones) = 25 € (hab)
27. The Truel. Pistoleros diferente puntería
Tres pistoleros. Duelo a muerte. El primero acierta 1 de cada 3 veces, el segundo acierta 2 de cada tres y el tercero siempre acierta.
Sólo puede quedar uno. Disparan por turnos. primero el primero, después el segundo, después el tercero y vuelta a empezar entre los que queden vivos. Un solo disparo en cada turno.
¿Cómo debe disparar el primero para que tenga las máximas probabilidades de salir con vida?
Solución
(No están bien hechos los cálculos de probabilidades)
- Si el primero falla intencionalmente y el segundo falla al tercero: Hay probabilidad de 1/6 de supervivencia para el primer. Aquí están los cálculos: 1 (1 falla intencionadamente) • 1/3 (probabilidades de que 2 falle con 3) • 1 (3 dispara a 2) • 1/3 (1 dispara a 3 como última oportunidad de eliminar a 3) = 1/6 = 0,16
- Si el primero falla intencionalmente y el segundo mata al tercero: El duelo podría continuar durante mucho más tiempo. Las matemáticas son un poco más complicadas: 1 (1 falla intencional) • 2/3 (probabilidades de que 2 acierte con 3), luego el 1 consigue un tiro con • 1/3 (en el mejor de los casos) = 2/9 = 0,22. Pero incluso si falla, no se garantiza que esté muerto, ya que el 2 podría fallar en el siguiente disparo y potencialmente podría continuar de un lado a otro durante muchos disparos. En cualquier caso la probabilidad bajaría.
- Conclusión: si el 1 dispara al aire inicialmente, tiene un 40 por ciento de posibilidades de sobrevivir. Si le dispara al 3, tiene cerca de un 31 por ciento de posibilidades de sobrevivir. Y si le dispara al 2, sus probabilidades son las peores, con aproximadamente un 26,5 por ciento de posibilidades de sobrevivir.
26. Cocktails
En un bar disponen de 9 cocktails diferentes. No conoces nada sobre ellos más que sus nombres: Aviation, Bronx, Caipirinha, Grasshopper, Hurricane, Kamikaze, Manhattan, Negroni y Vesper.
Tienes tres rondas de bebidas. En cada ronda podrás pedir y probar los 5 cocktails. El camarero, por supuesto, no te dirá cuál es cuál. Y también, por supuesto, eres capaz de recordar sabores.
¿Qué bebidas habrás de pedir en cada ronda para que al finalizar las tres rondas, hayas probado todos los cocktails y sepas reconocerlos?
Solución
PRIMERA RONDA: Aviation, Bronx, Caipirinha, Grasshopper, Grasshopper. Ahora puedes identificar al Grasshopper (pedido dos veces en esta ronda).
SEGUNDA RONDA: Aviation, Huracán, Kamikaze, Manhattan, Manhattan. Ahora puedes identificar el Manhattan (pedido dos veces en esta ronda) y el Aviation (única bebida pedida en la primera y segunda ronda).
RONDA TRES: Bronx, Hurricane, Negroni, Vesper, Vesper. Ahora puede identificar Vesper (pedido dos veces en esta ronda), Bronx (pedido de bebida pedido en la primera y tercera ronda), Hurricane (única bebida pedida en la segunda y tercera ronda), Caipirinha (única bebida no identificada de la primera ronda), Kamikaze (única bebida no identificada de la segunda ronda) y Negroni (única bebida no identificada de la tercera ronda).
25. Conductor de autobús
Estás conduciendo un autobús. El autobús comienza vacío… En la primera parada, suben dos personas. En la segunda parada, suben ocho personas y una persona se baja. En la tercera parada, suben tres personas y cinco personas se bajan. El autobús es amarillo, pero ¿de qué color es el pelo del conductor del autobús?
Solución
El que conduces eres tu
24. Aparcamiento Coche
¿En qué número de plaza está aparcado el coche?

Solución
87. Los número están al revés
23. Paradoja de Monty Hall
En un concurso, se te presentan 3 puertas, una de ellas esconde un coche y las otras dos esconden una cabra. Debes elegir una de las puertas y ganarás lo que haya detrás. Evidentemente quieres ganar el coche. Sin embargo, antes de abrirla, el presentador, que sabe donde está el premio, abre una de las otras dos puertas y muestra que detrás de ella hay una cabra. Ahora se te permite reconsiderar tu decisión y escoger otra de las puertas si lo deseas.
¿Tendrás más posibilidades de ganar el coche si cambias de puerta?
Solución
Cuando elijo la puerta, en promedio, dos de cada tres veces detrás de la puerta habrá una cabra. O sea, que la mayor parte de las veces habré elegido una puerta con cabra.
Como después el presentador me enseña una puerta con cabra, es razonable cambiar mi elección previa y así tendré 2/3 de probabilidades de ganar el coche frente a 1/3 si me quedo con la puerta inicial.
22. Dos caminos y 2 guardianes
Estás caminando por una carretera y llegas a una bifurcación. Un camino lleva a la muerte; el otro, a la felicidad eterna. No sabes cuál es cuál. En la bifurcación, te encuentras a dos guardianes que saben a dónde conduce cada uno de los caminos. Uno de los guardianes siempre dice la verdad y el otro siempre miente. Solo puedes hacer una pregunta a uno de ellos. ¿Cómo decidirías qué camino coger?
Solución
Si fueras tu compañero, ¿Qué camino dirías que lleva a la felicidad eterna?.
Digamos que el camino de la derecha lleva a la felicidad eterna. Tras hacer tu pregunta, ambos guardianes te dirán exactamente lo mismo: “Diría que el camino de la izquierda lleva a la felicidad eterna.
En cualquier caso, cogerías lo opuesto a lo que ambos dijeran, porque uno dice la verdad sobre lo que es mentira, y el otro miente sobre lo que es la verdad.
21. Apretón de manos
César y Noelia coinciden en un bar con otros 4 matrimonios. Algunas de las personas se conocen entre sí y otras no, así que cada persona saluda con un beso a cada una de las personas que conoce y con un apretón de manos a cada una de las personas que no conoce.
Noelia pregunta a las 9 personas cuántos apretones de manos dio cada uno, y curiosamente, cada uno de los 9 dio un número de apretones diferente.
¿Cuántos apretones de mano dio César?
Solución
Primero, tenemos que averiguar qué nueve respuestas escuchó Noelia de las otras nueve personas en la sala. Dado que las dos personas de cada pareja ya se conocen, como máximo, cualquier persona podría haberse apretado las manos con otras ocho personas (ya que solo se apretaron con personas que no conocen).
Así, dado que las nueve respuestas son distintas entre sí, Julia debe haber escuchado las respuestas: 0, 1, 2, 3, 4, 5, 6, 7, 8.
Comencemos llamando a la persona que apretó ocho manos Persona 8. Está claro que la Persona 8 apretó la mano de todos excepto del propio cónyuge de la Persona 8 (porque ya conoce a su cónyuge). Por lo tanto, todos, excepto el cónyuge de la Persona 8, apretó al menos una mano. ¡Por lo tanto, el cónyuge de la Persona 8 debe ser la persona que apretó cero manos! Ahora sabemos que la Persona 8 debe estar casada con la Persona 0.
Ahora consideremos a la Persona 7. Sabemos que no apretó la mano de la Persona 0 porque, bueno, la Persona 0 no apretó ninguna mano. Esto significa que dado que el cónyuge de la Persona 0 y la Persona 7 están fuera, la Persona 7 debe haberse saludado con la mano con las otras siete personas.
Ahora, como antes, esto significa que esas otras siete personas se saludaron con al menos dos personas (Persona 8 y Persona 7), lo que significa que la persona que se saludó con una sola persona debe ser el cónyuge de la Persona 7. Entonces concluimos que la Persona 7 debe estar casada con la Persona 1.
Podemos usar una lógica similar para concluir que la Persona 6 debe estar emparejada con la Persona 2, y que la Persona 5 debe estar con la Persona 3. Finalmente, llegamos a la última pareja restante: Uno de ellos es la Persona 4, y el otro ha chocado las manos con la Persona 8, la Persona 7, la Persona 6 y la Persona 5 o, en otras palabras, también cuatro personas. Por lo tanto, el cónyuge de la Persona 4 es otra Persona 4.
Dado que Noelia escuchó nueve respuestas diferentes y no escuchó a dos personas responder que ambas habían saludado cuatro veces, debe ser porque Noelia misma saludó cuatro veces. Además, también debe darse el caso de que César, su esposo, sea la Persona 4.
Así, tenemos nuestra respuesta: César tocó cuatro codos.
20. Diez monedas 2 montones
Existen 10 monedas sobre una mesa. Sabes que existen 4 que tienen la cara hacia arriba y que las otras 6 están de cruz.
No puedes mirar las monedas. Puedes darle la vuelta a todas las monedas que quieras.
El objetivo es separarlas en 2 montones de forma que en cada montón haya exactamente el mismo número de monedas de cara. No importa el tamaño que tenga cada montón.
Solución
Se separan 4 monedas en un montón y se les da la vuelta. En cada montón habrá el mismo número de monedas de cara.
(Daría igual el número de monedas que hubiera al principio, siempre hay que coger el número de monedas que coincide con el número de caras que sabes con certeza que están de cara)
19. Monedas falsas en hilera
Se tienen diez monedas indistinguibles en hilera. Se sabe que dos de ellas son falsas y están en posiciones consecutivas en la hilera. Eliges primero unas cuantas de estas 10 monedas. Posteriormente, eliges otras cuantas de nuevo entre las 10 monedas (pueden repetirse). Finalmente se te responderá cuántas de las que elegiste primero eran falsas y cuántas de las que elegiste después eran falsas. (Las respuestas solo se te darán después de haber elegido los dos conjuntos de monedas). ¿Qué conjunto de monedas eliges en cada elección para saber con certeza cuáles eran las monedas falsas?
Solución
Es posible. Primera pregunta: monedas 1,2,3,4,9; Segunda pregunta: monedas 1,2,7,8,9; [nº falsas 1a pregunta, nº falsas 2a pregunta] -> monedas; [0,0] -> 5,6; [0,1] -> 6,7; [0,2] -> 7,8; [1,0] -> 4,5; [1,1] -> 9,10; [1,2] -> 8,9; [2,0] -> 3,4; [2,1] -> 2,3; [2,2] -> 1,2;
18. Doce bolas 3 pesadas
Tienes 12 bolas numeradas del 1 al 12, idénticas entre sí, salvo que una de ellas pesa distinto (no se sabe si un poco más o un poco menos).
Dispones de una balanza para realizar solo tres pesadas.
¿Cómo adivinar cuál es la bola que pesa distinto y si pesa más o menos?
Solución
17. Dos cuerdas, 45 minutos
Tienes dos cuerdas recubiertas de aceite para ayudarlas a arder, cada una con un recubrimiento diferente. Cada cuerda tarda exactamente 1 hora en quemarse por completo. Sin embargo, las cuerdas no se queman a un ritmo constante; hay lugares donde se queman un poco más rápido y lugares donde se queman un poco más lento, pero siempre tardan 1 hora en quemarse enteras.
Con un mechero para encender las cuerdas, ¿Cómo se pueden medir exactamente 45 minutos?
Solución
Quemas por los dos extremos de una cuerda y por uno de los extremos de la otra.
Cuando la primera cuerda se haya quemado por completo habrán pasado 30 minutos. En ese instante enciendes el extremo que falta de la cuerda que está todavía a medio arder. Tras 15 minutos más se quemará por completo.
16. Barca con zorro, gallina y maíz
Un hombre tiene que cruzar un río con un zorro, una gallina y un saco de maíz.
Tiene una barca de remos, y sólo puede llevar con él una cosa en la barca.
Si el zorro y la gallina se quedan solos, el zorro se come a la gallina.
Si la gallina y el maíz quedan solos, la gallina se come el maíz.
¿Cómo lo consigue el hombre?
Solución
El hombre y la gallina cruzan el río (el zorro y el maíz están seguros juntos), deja a la gallina al otro lado y cruza de vuelta.
Entonces toma el zorro al otro lado del río, y como no puede dejarlo con la gallina, se la trae de vuelta.
Igualmente, como la gallina y el maíz no pueden quedar solos, deja a la gallina y cruza con el maíz donde está el zorro.
Después vuelve a por la gallina y cruza con ella por última vez.
15. Diez cajas de 10 bolas
Tenemos 10 cajas con bolas de billar; cada caja pesa 10kg y contiene 10 bolas de billar (1kg cada una). Pero, una de las cajas salió defectuosa, aunque todas sus bolas pesan lo mismo, la caja completa pesa 9kg. Es decir, en una de las cajas, todas la bolas pesan 900 gramos.
Tenemos una sola oportunidad de utilizar una báscula electrónica para que diga el peso puesto sobre ella. Cómo podemos determinar, cuál caja es la de menor peso.
Solución
Numeramos las cajas del 1 al 10 y colocamos en la báscula el mismo numero de bolas que numero asignado. El resultado será 55 kilos, menos la diferencia que generan las bolas desiguales al resto, 100 gramos menos por cada bola.si pesara 54900g seria la caja 1, si pesara 54800g seria la caja 2 etc. La caja 10 se podría ausentar en todo el proceso y el resultado seria 45kilos, menos la diferencia de 100 gramos por bola diferente, a no ser que la caja diferente fuese la caja 10, cuyo resultado seria 45 kilos igualmente.
14. Tres parejas y río
Tres parejas y una barca de 2 personas para cruzar el río. No pueden ir juntos hombre y mujer si no son pareja. ¿Cuál es el número mínimo de viajes?
Solución
Cruce 1: Chloe y el agente de Chloe reman hasta el otro lado del río.
Cruce 2: El agente de Chloe se baja y Chloe rema hacia el lado más cercano.
Cruce 3: el agente de Lexa y el agente de Jon se van al otro lado.
Cruce 5: el agente de Lexa cambia de lugar con Jon y Chloe, quienes reman hacia el otro lado.
Cruce 6: Jon se baja y Chloe rema hacia el lado más cercano.
Cruce 7: Chloe cambia de lugar con Lexa y su agente, quienes reman hacia el otro lado.
Cruce 8: El agente de Chloe vuelve al bote y rema hacia el lado más cercano.
Cruce 9: Chloe y su agente reman hasta el otro lado. ¡Todos lo han logrado!
13. Distancia paralelopipedo
¿Cuál es la distancia más corta entre los puntos inicial y final?. ¿Y si solo se pudiera ir por el exterior?
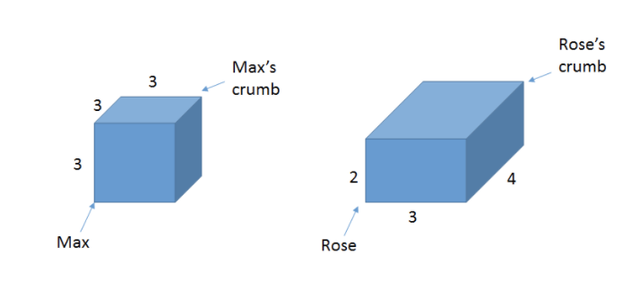
Solución
La forma más sencilla de encontrar esta ruta es aplanar la figura.
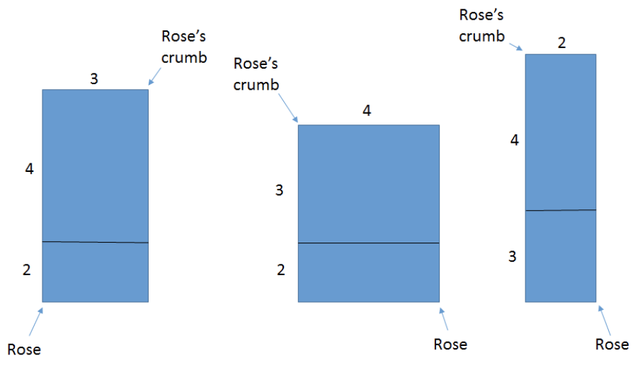
El teorema de Pitágoras, nos dirá que la diagonal del segundo rectángulo es la más corta con √41 o 6,41 cm.
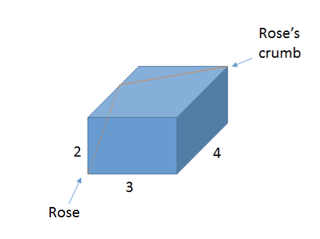
12. Proporcionalidad triple
Si 2 albañiles, construyen 2 muros en 2 días, ¿Cuántos muros construye cada albañil al día?
Solución
0,5
11. Hermanas y hermanos
El señor y la señora García tienen seis hijas y cada hija tiene un hermano. ¿Cuántas personas hay en la familia García?.
Solución
Como cada hija comparte el mismo hermano, hay seis chicas, un chico y el señor y la señora García.
10. Abuelo con nietos
Mi abuelo tiene 5 hijos y cada hijo tiene 3 hijos. ¿Cuántos primos tengo?
Solución
Tengo 12 primos (4 x 3 = 12), porque uno de los hijos de tu abuelo es tu padre, quien tiene 3 hijos (tú y tus 2 hermanos).
9. Cinco hijas
La mamá de Rosa tiene cinco hijas: pata, peta, pita, pota, ¿y?, …
Solución
Rosa
8. Reparto naranjas
Pedro y Lupe tienen unas naranjas. Si Pedro le da una naranja a Lupe, los dos tendrán igual cantidad de naranjas. Si Lupe le da una naranja a Pedro, este tendrá el doble de naranjas que Lupe. ¿Cuántas naranjas tienen cada uno?
Solución
Pedro tiene 7 naranjas y Lupe tiene 5 naranjas
7. Llenar botella con otras 2
Tienes dos botellas vacías, una de 3 litros y otra de 5 litros. ¿Cómo haces para medir un litro de agua?
Solución
Tienes que llenar la botella de 3 litros y vaciarla en la de 5 litros; luego rellenar la botella de 3 litros y verterla en la de 5 litros hasta que esté llena. Te quedará 1 litro de agua en la botella de 3 litros.
6. Boinas blancas y negras
El director de una prisión llama a tres de sus presos, les enseña tres boinas blancas y dos boinas negras, y les dice: «Voy a colocar a cada uno de ustedes una boina en la cabeza, el primero de ustedes que me indique el color de la suya será puesto en libertad y si se equivoca será castigado».
Los presos están en fila, de manera que el primero no puede ver las boinas de los otros dos, el segundo ve la boina del primero y el tercero ve las boinas de los otros dos.
Tras unos momentos de tenso silencio, el primero de ellos acierta el color. ¿De qué color tenía la boina?. ¿Cómo lo pudo saber?
Solución
Como el tercer preso, que ve las dos boinas, no dice nada inmediatamente, es porque no ha visto dos boinas negras. Si el segundo viera una boina negra en el primero, sabría que él tiene una blanca ya que no oye al tercero decir que tiene una blanca. Entonces el primer preso tiene una boina blanca.
5. Tres canastos con frutas
Tienes 3 canastas: una que contiene naranjas, otra que contiene manzanas y otra que contiene naranjas y manzanas. Una canasta está etiquetada como “manzanas”, la otra como “naranjas” y la última como “manzanas y naranjas”. Se sabe con certeza que las tres etiquetas están mal puestas. Se te permite coger una sola fruta de una de las canastas (sin mirar, obviamente, el resto del contenido de la canasta). Tras observar lo que eliges, tendrás que etiquetar correctamente cada canasta. ¿Cómo lo harías?
Solución
Dado que se garantiza que cada canasta está etiquetada incorrectamente, todo lo que tienes que hacer es coger una fruta de la canasta con la etiqueta “Manzanas y naranjas”. Si sacas una naranja, entonces esta canasta es la canasta de naranjas. Si sacas una manzana, entonces es la canasta de manzanas.
A continuación, busca la cesta etiquetada con la otra fruta: esta canasta tendrá ambas frutas (naranjas y manzanas).
La canasta final contiene la fruta que no has sacado en la primera canasta.
4. Tres bolsas y 12 canicas
Tienes 12 canicas y 3 grandes bolsas idénticas. ¿Cómo conseguirías que haya exactamente el mismo número de canicas en cada bolsa?. (A parte de 4 canicas en cada bolsa)
Solución
Metes las 12 canicas en una bolsa, metes esa bolsa en una de las otras bolsas y ésta a su vez en la tercera bolsa.
3. Cruzar puente y 4 personas una sola linterna
Cuatro personas llegan a un río con un puente estrecho que solo aguanta el peso de dos personas al mismo tiempo. Es de noche, y tienen una linterna que tienen que usar para cruzar el puente. La persona A puede cruzar el puente en 1 minuto, B en 2 minutos, C en 5 minutos y D en 8 minutos. Cuando dos personas cruzan el puente juntos, tienen que caminar al paso de la persona más lenta. ¿Cuál es el tiempo mínimo para que todos crucen el puente?
Solución
- Primero, A y B cruzan el puente y A lleva la linterna de vuelta. Esto lleva 3 minutos.
- Luego, C y D cruzan el puente y B lleva la linterna de vuelta. Esto lleva 10 minutos.
- Finalmente, A y B vuelven a cruzar. Esto lleva otros 2 minutos.
2. Huevo en 15 minutos con reloj de arena
Si tienes un reloj de arena de 7 minutos, y un reloj de arena de 11 minutos, ¿cómo puedes hervir un huevo en exactamente 15 minutos?
Solución
- Dale la vuelta a ambos relojes de arena cuando empieces a hervir el huevo.
- Cuando se agote el reloj de 7 minutos, dale la vuelta para que empiece de nuevo.
- Cuatro minutos más tarde, cuando se agote el reloj de 11 minutos, dale la vuelta de nuevo al de 7 minutos.
- Espera a que se agote el de los 7 minutos de nuevo, que llevará otros 4 minutos, y en total habrás alcanzado exactamente 15 minutos.
1. Depósito que se duplica
En un depósito, hay un nivel de agua muy bajo pero que se duplica todos los días. Tarda 10 días en llenarse. ¿Cuánto tarda en llegar a la mitad?
Solución
9 días